Теория алгоритмов

Машина Тьюринга и алгоритмически неразрешимые проблемы

  1. Машина Тьюринга

    Алан Тьюринг (Turing) в 1936 году опубликовал в трудах Лондонского математического общества статью «О вычислимых числах в приложении к проблеме разрешения», которая наравне с работами Поста и Черча лежит в основе современной теории алгоритмов.

    Предыстория создания этой работы связана с формулировкой Давидом Гильбертом на Международном математическом конгрессе в Париже в 1900 году неразрешенных математических проблем. Одной из них была задача до-казательства непротиворечивости системы аксиом обычной арифметики, которую Гильберт в дальнейшем уточнил как «проблему разрешимости» - нахождение общего метода, для определения выполнимости данного высказывания на языке формальной логики.

    Статья Тьюринга как раз и давала ответ на эту проблему - вторая про-блема Гильберта оказалась неразрешимой. Но значение статьи Тьюринга выходило далеко за рамки той задачи, по поводу которой она была написана.

    Приведем характеристику этой работы, принадлежащую Джону Хоп-крофту: «Работая над проблемой Гильберта, Тьюрингу пришлось дать четкое определение самого понятия метода. Отталкиваясь от интуитивного представления о методе как о некоем алгоритме, т.е. процедуре, которая может быть выполнена механически, без творческого вмешательства, он показал, как эту идею можно воплотить в виде подробной модели вычислительного процесса. Полученная модель вычислений, в которой каждый алгоритм разбивался на последовательность простых, элементарных шагов, и была логической конструкцией, названной впоследствии машиной Тьюринга».

    Машина Тьюринга является расширением модели конечного автомата, расширением, включающим потенциально бесконечную память с возможностью перехода (движения) от обозреваемой в данный момент ячейки к ее левому или правому соседу.

      Формально машина Тьюринга может быть описана следующим образом: Пусть заданы:

    • конечное множество состояний – Q, в которых может находиться машина Тьюринга;

    • конечное множество символов ленты – Г;

    • функция 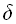(функция переходов или программа), которая задается отображением пары из декартова произведения Q x Г (машина находится в состоянии 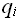и обозревает символ 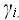) в тройку декартова произведения Q х Г х {L,R} (машина переходит в состояние 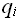, заменяет символ 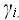на символ 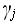и передвигается влево или вправо на один символ ленты) – Q x Г-->Q х Г х {L,R}

    • один символ из Г-->е (пустой);

    • подмножество 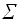є Г --> определяется как подмножество входных символов ленты, причем е є (Г-);

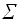    • одно из состояний – 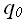є Q является начальным состоянием машины.

    Решаемая проблема задается путем записи конечного количества символов из множества 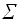є Г – Si є 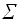на ленту:
    eS1S2S3S4.........Sne

    после чего машина переводится в начальное состояние и головка устанавливается у самого левого непустого символа – 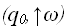, после чего в соответствии с указанной функцией переходов (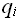, 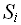)-->(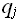,,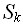 L или R) машина начинает заменять обозреваемые символы, передвигать головку вправо или влево и переходить в другие состояния, предписанные функций переходов.

    Остановка машины происходит в том случае, если для пары (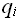,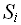) функ-ция перехода не определена.

    Алан Тьюринг высказал предположение, что любой алгоритм в интуитивном смысле этого слова может быть представлен эквивалентной машиной Тьюринга. Это предположение известно как тезис Черча–Тьюринга. Каждый компьютер может моделировать машину Тьюринга (операции перезаписи ячеек, сравнения и перехода к другой соседней ячейке с учетом изменения состояния машины). Следовательно, он может моделировать алгоритмы в любом формализме, и из этого тезиса следует, что все компьютеры (независимо от мощности, архитектуры и т.д.) эквивалентны с точки зрения принципиальной возможности решения алгоритмических задач.

  2. Алгоритмически неразрешимые проблемы

    За время своего существования человечество придумало множество алгоритмов для решения разнообразных практических и научных проблем. Зададимся вопросом – а существуют ли какие-нибудь проблемы, для которых невозможно придумать алгоритмы их решения?

    Утверждение о существовании алгоритмически неразрешимых проблем является весьма сильным – мы констатируем, что мы не только сейчас на знаем соответствующего алгоритма, но мы не можем принципиально никогда его найти.

    Успехи математики к концу XIX века привели к формированию мнения, которое выразил Д. Гильберт – «в математике не может быть неразрешимых проблем», в связи с этим формулировка проблем Гильбертом на конгрессе 1900 года в Париже была руководством к действию, констатацией отсутствия решений в данный момент.

    Первой фундаментальной теоретической работой, связанной с доказательством алгоритмической неразрешимости, была работа Курта Гёделя – его известная теорема о неполноте символических логик. Это была строго формулированная математическая проблема, для которой не существует решающего ее алгоритма. Усилиями различных исследователей список алгоритмически неразрешимых проблем был значительно расширен. Сегодня принято при доказательстве алгоритмической неразрешимости некоторой задачи сводить ее к ставшей классической задаче – «задаче останова».

    Имеет место быть следующая теорема:

    Теорема 3.1. Не существует алгоритма (машины Тьюринга), позволяющего по описанию произвольного алгоритма и его исходных данных (и алго-ритм и данные заданы символами на ленте машины Тьюринга) определить, останавливается ли этот алгоритм на этих данных или работает бесконечно.

    Таким образом, фундаментально алгоритмическая неразрешимость связана с бесконечностью выполняемых алгоритмом действий, т.е. невозможностью предсказать, что для любых исходных данных решение будет получено за конечное количество шагов.

    Тем не менее, можно попытаться сформулировать причины, ведущие к алгоритмической неразрешимости, эти причины достаточно условны, так как все они сводимы к проблеме останова, однако такой подход позволяет более глубоко понять природу алгоритмической неразрешимости:

    а) Отсутствие общего метода решения задачи

    Проблема 1: Распределение девяток в записи числа ;

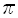    Определим функцию f(n) = i, где n – количество девяток подряд в десятичной записи числа 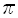, а i – номер самой левой девятки из n девяток подряд: 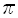=3,141592… f(1) = 5.

    Задача состоит в вычислении функции f(n) для произвольно заданного n.

    Поскольку число 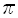является иррациональным и трансцендентным, то мы не знаем никакой информации о распределении девяток (равно как и любых других цифр) в десятичной записи числа 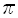. Вычисление f(n) связано с вычислением последующих цифр в разложении 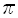, до тех пор, пока мы не обнаружим n девяток подряд, однако у нас нет общего метода вычисления f(n), поэтому для некоторых n вычисления могут продолжаться бесконечно – мы даже не знаем в принципе (по природе числа 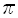) существует ли решение для всех n.

    Проблема 2: Вычисление совершенных чисел;

    Совершенные числа – это числа, которые равны сумме своих делителей, например: 28 = 1+2+4+7+14.

    Определим функцию S(n) = n-ое по счёту совершенное число и поставим задачу вычисления S(n) по произвольно заданному n. Нет общего метода вы-числения совершенных чисел, мы даже не знаем, множество совершенных чи-сел конечно или счетно, поэтому наш алгоритм должен перебирать все числа подряд, проверяя их на совершенность. Отсутствие общего метода решения не позволяет ответить на вопрос о останове алгоритма. Если мы проверили М чи-сел при поиске n-ого совершенного числа – означает ли это, что его вообще не существует?

    Проблема 3: Десятая проблема Гильберта;

    Пусть задан многочлен n-ой степени с целыми коэффициентами – P, су-ществует ли алгоритм, который определяет, имеет ли уравнение P=0 решение в целых числах?

    Ю.В. Матиясевич показал, что такого алгоритма не существует, т.е. отсутствует общий метод определения целых корней уравнения P=0 по его целочисленным коэффициентам.

    б) Информационная неопределенность задачи

    Проблема 4: Позиционирование машины Поста на последний помеченный ящик;

    Пусть на ленте машины Поста заданы наборы помеченных ящиков (кортежи) произвольной длины с произвольными расстояниями между кортежами и головка находится у самого левого помеченного ящика. Задача состоит установке головки на самый правый помеченный ящик последнего кортежа.

    Попытка построения алгоритма, решающего эту задачу приводит к необходимости ответа на вопрос – когда после обнаружения конца кортежа мы сдвинулись вправо по пустым ящикам на М позиций и не обнаружили начало следующего кортежа – больше на ленте кортежей нет или они есть где-то правее? Информационная неопределенность задачи состоит в отсутствии информации либо о количестве кортежей на ленте, либо о максимальном расстоянии между кортежами – при наличии такой информации (при разрешении инфор-мационной неопределенности) задача становится алгоритмически разрешимой.

    в) Логическая неразрешимость (в смысле теоремы Гёделя о неполноте)

    Проблема 5: Проблема «останова» (см. теорема 3.1);

    Проблема 6: Проблема эквивалентности алгоритмов;

    По двум произвольным заданным алгоритмам (например, по двум машинам Тьюринга) определить, будут ли они выдавать одинаковые выходные результаты на любых исходных данных.

    Проблема 7: Проблема тотальности;

    По произвольному заданному алгоритму определить, будет ли он останавливаться на всех возможных наборах исходных данных. Другая формулировка этой задачи – является ли частичный алгоритм Р всюду определённым?

  3. Проблема соответствий Поста над алфавитом

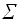
    В качестве более подробного примера алгоритмически неразрешимой задачи рассмотрим проблему соответствий Поста (Э. Пост, 1943 г.). Мы выделили эту задачу, поскольку на первый взгляд она выглядит достаточно «алгоритмизуемой», однако она сводима к проблеме останова и является алго-ритмически неразрешимой.

    Постановка задачи:

    Пусть дан алфавит 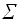: ||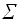 >= 2 (для односимвольного алфавита задача имеет решение) и дано конечное множество пар из 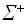х 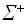, т.е. пары непустых цепочек произвольного языка над алфавитом : , ……, .

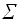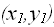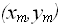    Проблема: Выяснить существует ли конечная последовательность этих пар, не обязательно различных, такая что цепочка, составленная из левых подцепочек, совпадает с последовательностью правых подцепочек – такая последовательность называется решающей.

    В качестве примера рассмотрим 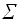= {a,b}

    1. Входные цепочки: (abbb, b), (a, aab), (ba, b)

    Решающая последовательность для этой задачи имеет вид:

    (a,aab) (a,aab) (ba,b) (abbb,b), так как : a a ba abbb 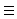aab aab b b

    2. Входные цепочки: (ab,aba), (aba,baa), (baa,aa)

    Данная задача вообще не имеет решения, так как нельзя начинать с пары (aba,baa) или (baa,aa), поскольку не совпадают начальные символы подцепочек, но если начинать с цепочки (ab,aba), то в последующем не будет совпадать общее количество символов «а», т.к. в других двух парах количество символов «а» одинаково.

    В общем случае мы можем построить частичный алгоритм, основанный на идее упорядоченной генерации возможных последовательностей цепочек (отметим, что мы имеем счетное множество таких последовательностей) с проверкой выполнения условий задачи. Если последовательность является решающей – то мы получаем результативный ответ за конечное количество шагов. Поскольку общий метод определения отсутствия решающей последовательности не может быть указан, т.к. задача сводима к проблеме «останова» и, следовательно, является алгоритмически неразрешимой, то при отсутствии решающей последовательности алгоритм порождает бесконечный цикл.

    В теории алгоритмов такого рода проблемы, для которых может быть предложен частичный алгоритм их решения, частичный в том смысле, что он возможно, но не обязательно, за конечное количество шагов находит решение проблемы, называются частично разрешимыми проблемами.

    В частности, проблема останова так же является частично разрешимой проблемой, а проблемы эквивалентности и тотальности не являются таковыми.

Rambler's Top100
Hosted by uCoz