Теория алгоритмов
Введение в анализ алгоритмов
Сравнительные оценки алгоритмов
При использовании алгоритмов для решения практических задач мы сталкиваемся с проблемой рационального выбора алгоритма решения задачи. Решение проблемы выбора связано с построением системы сравнительных оценок, которая в свою очередь существенно опирается на формальную модель алгоритма.
Будем рассматривать в дальнейшем, придерживаясь определений Поста, применимые к общей проблеме, правильные и финитные алгоритмы, т.е. алго-ритмы, дающие 1-решение общей проблемы. В качестве формальной системы будем рассматривать абстрактную машину, включающую процессор с фонНеймановской архитектурой, поддерживающий адресную память и набор «элементарных» операций соотнесенных с языком высокого уровня.
-
В целях дальнейшего анализа примем следующие допущения:
каждая команда выполняется не более чем за фиксированное время;
исходные данные алгоритма представляются машинными словами по
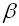 битов каждое.
битов каждое.
Конкретная проблема задается N словами памяти, таким образом, на входе алгоритма –
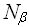 = N*
= N*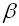 бит информации. Отметим, что в ряде случаев, особенно при рассмотрении матричных задач N является мерой длины входа алгоритма, отражающей линейную размерность.
бит информации. Отметим, что в ряде случаев, особенно при рассмотрении матричных задач N является мерой длины входа алгоритма, отражающей линейную размерность.Программа, реализующая алгоритм для решения общей проблемы состоит из М машинных инструкций по
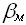 битов –
битов – 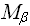 = М*
= М*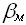 бит информации.
бит информации.-
Кроме того, алгоритм может требовать следующих дополнительных ресурсов абстрактной машины:
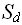 – память для хранения промежуточных результатов;
– память для хранения промежуточных результатов;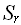 – память для организации вычислительного процесса (память, необходимая для реализации рекурсивных вызовов и возвратов).
– память для организации вычислительного процесса (память, необходимая для реализации рекурсивных вызовов и возвратов).
При решении конкретной проблемы, заданной N словами памяти алгоритм выполняет не более, чем конечное количество «элементарных» операций абстрактной машины в силу условия рассмотрения только финитных алгоритмов. В связи с этим введем следующее определение:
Определение 4.1. Трудоёмкость алгоритма.
Под трудоёмкостью алгоритма для данного конкретного входа –
 (N), будем понимать количество «элементарных» операций совершаемых алгоритмом для решения конкретной проблемы в данной формальной системе.
(N), будем понимать количество «элементарных» операций совершаемых алгоритмом для решения конкретной проблемы в данной формальной системе.Комплексный анализ алгоритма может быть выполнен на основе комплексной оценки ресурсов формальной системы, требуемых алгоритмом для решения конкретных проблем. Очевидно, что для различных областей применения веса ресурсов будут различны, что приводит к следующей комплексной оценке алгоритма:
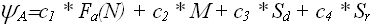 , где
, где 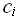 – веса ресурсов.
– веса ресурсов.Система обозначений в анализе алгоритмов
При более детальном анализе трудоемкости алгоритма оказывается, что не всегда количество элементарных операций, выполняемых алгоритмом на одном входе длины N, совпадает с количеством операций на другом входе такой же длины. Это приводит к необходимости введения специальных обозначений, отражающих поведение функции трудоемкости данного алгоритма на входных данных фиксированной длины.
Пусть
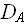 – множество конкретных проблем данной задачи, заданное в формальной системе. Пусть D є
– множество конкретных проблем данной задачи, заданное в формальной системе. Пусть D є 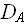 – задание конкретной проблемы и |D| = N.
– задание конкретной проблемы и |D| = N.В общем случае существует собственное подмножество множества
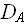 , включающее все конкретные проблемы, имеющие мощность N:
, включающее все конкретные проблемы, имеющие мощность N:обозначим это подмножество через
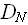 :
: 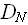 = {D є
= {D є 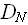 ,: |D| = N};
,: |D| = N};обозначим мощность множества
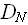 через
через 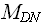 -->
--> 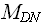 = |
= |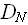 |.
|.-
Тогда содержательно данный алгоритм, решая различные задачи размерности N, будет выполнять в каком-то случае наибольшее количество операций, а в каком-то случае наименьшее количество операций. Ведем следующие обозначения:
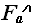 (N) – худший случай – наибольшее количество операций, совершаемых алгоритмом А для решения конкретных проблем размерностью N:
(N) – худший случай – наибольшее количество операций, совершаемых алгоритмом А для решения конкретных проблем размерностью N: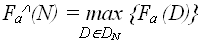 - худший случай на
- худший случай на 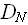
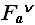 (N) – лучший случай – наименьшее количество операций, совершаемых алгоритмом А для решения конкретных проблем размерностью N:
(N) – лучший случай – наименьшее количество операций, совершаемых алгоритмом А для решения конкретных проблем размерностью N: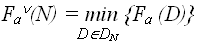 – лучший случай на
– лучший случай на 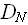
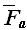 (N) – средний случай – среднее количество операций, совершаемых алгоритмом А для решения конкретных проблем размерностью N:
(N) – средний случай – среднее количество операций, совершаемых алгоритмом А для решения конкретных проблем размерностью N: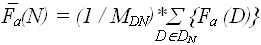 – средний случай на
– средний случай на 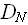
Классификация алгоритмов по виду функции трудоёмкости
В зависимости от влияния исходных данных на функцию трудоемкости алгоритма может быть предложена следующая классификация, имеющая практическое значение для анализа алгоритмов:
1.Количественно-зависимые по трудоемкости алгоритмы
Это алгоритмы, функция трудоемкости которых зависит только от размерности конкретного входа, и не зависит от конкретных значений:
 (D) =
(D) =  (|D|) =
(|D|) =  (N)
(N)Примерами алгоритмов с количественно-зависимой функцией трудоемкости могут служить алгоритмы для стандартных операций с массивами и матрицами – умножение матриц, умножение матрицы на вектор и т.д.
2.Параметрически-зависимые по трудоемкости алгоритмы
Это алгоритмы, трудоемкость которых определяется не размерностью входа (как правило, для этой группы размерность входа обычно фиксирована), а конкретными значениями обрабатываемых слов памяти:
 (D) =
(D) =  (
(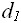 ,…,
,…,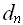 ) =
) =
 (
(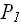 ,…,
,…,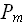 ), m =< n
), m =< nПримерами алгоритмов с параметрически-зависимой трудоемкостью являются алгоритмы вычисления стандартных функций с заданной точностью путем вычисления соответствующих степенных рядов. Очевидно, что такие алгоритмы, имея на входе два числовых значения – аргумент функции и точность выполняют существенно зависящее от значений количество операций.
а) Вычисление
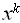 последовательным умножением
последовательным умножением 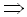
 (x, k) =
(x, k) =  (k).
(k).б) Вычисление
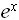 =
= 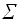 (
(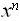 /n!), с точностью до
/n!), с точностью до 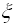
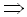
 =
=  (x,
(x, 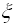 )
)3. Количественно-параметрические по трудоемкости алгоритмы
Однако в большинстве практических случаев функция трудоемкости зависит как от количества данных на входе, так и от значений входных данных, в этом случае:
 (D) =
(D) =  (||D||,
(||D||, 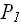 ,…,
,…,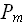 ) =
) =  (N,
(N, 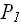 ,…,
,…,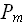 )
)В качестве примера можно привести алгоритмы численных методов, в которых параметрически-зависимый внешний цикл по точности включает в себя количественно-зависимый фрагмент по размерности.
3.1 Порядково-зависимые по трудоемкости алгоритмы
Среди разнообразия параметрически-зависимых алгоритмов выделим еще оду группу, для которой количество операций зависит от порядка распо-ложения исходных объектов.
Пусть множество D состоит из элементов (
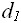 ,…,
,…,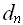 ), и ||D||=N,
), и ||D||=N,Определим
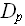 = {(
= {(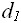 ,…,
,…,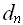 )}-множество всех упорядоченных N-ок из
)}-множество всех упорядоченных N-ок из 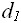 ,…,
,…,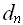 , отметим, что |
, отметим, что |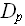 |=n!.
|=n!.Если
 (i
(i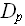 )
) 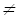
 (j
(j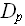 ), где i
), где i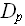 , j
, j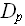 є
є 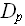 , то алгоритм будем называть порядково-зависимым по трудоемкости.
, то алгоритм будем называть порядково-зависимым по трудоемкости.Примерами таких алгоритмов могут служить ряд алгоритмов сортировки, алгоритмы поиска минимума и максимума в массиве. Рассмотрим более подробно алгоритм поиска максимума в массиве S, содержащим n элементов:
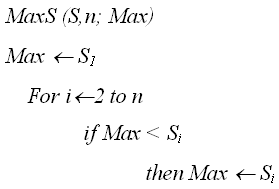
(количество выполненных операций присваивания зависит от порядка следования элементов массива)
Асимптотический анализ функций
При анализе поведения функции трудоемкости алгоритма часто используют принятые в математике асимптотические обозначения, позволяющие по-казать скорость роста функции, маскируя при этом конкретные коэффициенты.
Такая оценка функции трудоемкости алгоритма называется сложностью алгоритма и позволяет определить предпочтения в использовании того или иного алгоритма для больших значений размерности исходных данных.
В асимптотическом анализе приняты следующие обозначения:
1. Оценка
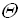 (тетта)
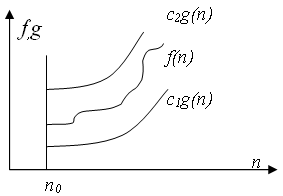
(тетта)Пусть f(n) и g(n) – положительные функции положительного аргумента, n >= 1 (количество объектов на входе и количество операций – положительные числа), тогда:
f(n) =
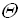 (g(n)), если существуют положительные с1, с2, n0, такие, что:
(g(n)), если существуют положительные с1, с2, n0, такие, что:
с1 * g(n) =< f(n) =< c2 * g(n),
при n > n0Обычно говорят, что при этом функция g(n) является асимптотически точной оценкой функции f(n), т.к. по определению функция f(n) не отличается от функции g(n) с точностью до постоянного множителя.
Отметим, что из f(n) =
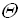 (g(n)) следует, что g(n) =
(g(n)) следует, что g(n) = 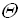 (f(n)).
(f(n)).Примеры:
1) f(n)=4
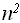 +nlnN+174 – f(n)=
+nlnN+174 – f(n)= 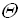 (
(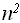 );
);2) f(n)=
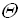 (1) – запись означает, что f(n) или равна константе, не равной нулю, или f(n) ограничена константой на
(1) – запись означает, что f(n) или равна константе, не равной нулю, или f(n) ограничена константой на 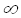 : f(n) = 7+1/n =
: f(n) = 7+1/n = 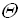 (1).
(1).2. Оценка О (О большое)
В отличие от оценки
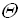 , оценка О требует только, что бы функция f(n) не превышала g(n) начиная с n > n0, с точностью до постоянного множителя:
, оценка О требует только, что бы функция f(n) не превышала g(n) начиная с n > n0, с точностью до постоянного множителя: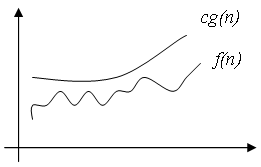
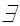 c > 0, n0 > 0 :
0 =< f(n) =< c * g(n),
c > 0, n0 > 0 :
0 =< f(n) =< c * g(n), 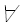 n > n0
n > n0Вообще, запись O(g(n)) обозначает класс функций, таких, что все они растут не быстрее, чем функция g(n) с точностью до постоянного множителя, поэтому иногда говорят, что g(n) мажорирует функцию f(n).
Например, для всех функций:
f(n)=1/n, f(n)= 12, f(n)=3*n+17, f(n)=n*Ln(n), f(n)=6*
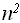 +24*n+77 будет справедлива оценка О(
+24*n+77 будет справедлива оценка О(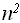 )
)Указывая оценку О есть смысл указывать наиболее «близкую» мажорирующую функцию, поскольку например для f(n)=
3. Оценка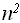 справедлива оценка О(
справедлива оценка О(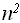 ), однако она не имеет практического смысла.
), однако она не имеет практического смысла.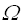 (Омега)
(Омега)
В отличие от оценки О, оценка
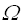 является оценкой снизу – т.е. определяет класс функций, которые растут не медленнее, чем g(n) с точностью до постоянного множителя:
является оценкой снизу – т.е. определяет класс функций, которые растут не медленнее, чем g(n) с точностью до постоянного множителя: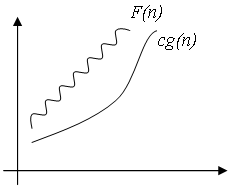
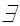 c > 0, n0 >0 : 0 =< c * g(n) =< f(n)
c > 0, n0 >0 : 0 =< c * g(n) =< f(n)Например, запись
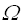 (n*Ln(n)) обозначает класс функций, которые растут не медленнее, чем g(n) = n*Ln(n), в этот класс попадают все полиномы со степенью большей единицы, равно как и все степенные функции с основанием большим единицы.
(n*Ln(n)) обозначает класс функций, которые растут не медленнее, чем g(n) = n*Ln(n), в этот класс попадают все полиномы со степенью большей единицы, равно как и все степенные функции с основанием большим единицы.Асимптотическое обозначение О восходит к учебнику Бахмана по теории простых чисел (Bachman, 1892), обозначения
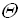 ,
, 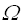 введены Д. Кнутом (Donald Knuth).
введены Д. Кнутом (Donald Knuth).Отметим, что не всегда для пары функций справедливо одно из асимптотических соотношений, например для f(n)=
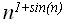 и g(n)=n не выполняется ни одно из асимптотических соотношений.
и g(n)=n не выполняется ни одно из асимптотических соотношений.В асимптотическом анализе алгоритмов разработаны специальные методы получения асимптотических оценок, особенно для класса рекурсивных алгоритмов. Очевидно, что
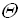 оценка является более прдпочтительной, чем оценка О. Знание асимптотики поведения функции трудоемкости алгоритма - его сложности, дает возможность делать прогнозы по выбору более рационального с точки зрения трудоемкости алгоритма для больших размерностей исходных данных.
оценка является более прдпочтительной, чем оценка О. Знание асимптотики поведения функции трудоемкости алгоритма - его сложности, дает возможность делать прогнозы по выбору более рационального с точки зрения трудоемкости алгоритма для больших размерностей исходных данных.

