Теория алгоритмов
Рекурсивные функции и алгоритмы
Рекурсивные функции
а) Терминологическое введение
По сути один и тот же метод, применительно к различным областям носит различные названия – это индукция, рекурсия и рекуррентные соотношения – различия касаются особенностей использования.
Под индукцией понимается метод доказательства утверждений, который строится на базе индукции при n=0,1, затем утверждение полагается правильным при n=n b и проводится доказательство для n+1.
Под рекурсией понимается метод определения функции через её предыдущие и ранее определенные значения, а так же способ организации вычислений, при котором функция вызывает сама себя с другим аргументом.
Термин рекуррентные соотношения связан с американским научным стилем и определяет математическое задание функции с помощью рекурсии.
Основной задачей исследования рекурсивно заданных функций является получение f(n) в явной или как еще говорят «замкнутой» форме, т.е. в виде аналитически заданной функции. В связи с этим рассмотрим ряд примеров:
б) Примеры рекурсивного задания функций
1. 
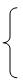
f(0)=0
f(n)= f(n-1)+12. 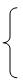f(0)=1
f(n)= n*f(n-1)Последовательная подстановка дает – f(n)=1*2*3*…*n = n!
Для полноты сведений приведем формулу Стирлинга для приближенного вычисления факториала для больших n:
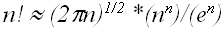
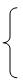
3. f(0)=1
f(1)=1
f(n)= f(n-1)+ f(n-2), n>=2Эта рекурсивная функция определяет числа Фибоначчи: 1 1 2 3 5 8 13, которые достаточно часто возникают при анализе различных задач, в том числе и при анализе алгоритмов. Отметим, что асимптотически
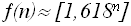
4. f(0)=1
f(n)= f(n-1)+ f(n-2)+…+1 =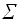
f(i)+1
Для получения функции в явном виде рассмотрим ее последовательные значения:f(0)=1, f(1)=2, f(2)=4, f(3)=8, что позволяет предположить, что f(n)=
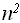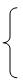
, точное доказательство выполняется по индукции.5. f(0)=1
f(n)= 2*f(n-1)Мы имеем дело с примером того, что одна и та же функция может иметь различные рекурсивные определения – f(n)=
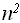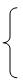
, как и в примере 4, что проверяется элементарной подстановкой.6. f(0)=1
f(1)=2
f(n)= f(n-1)*f(n-2)В этом случае мы можем получить решение в замкнутой форме, сопоставив значениям функции соответствующие степени двойки:
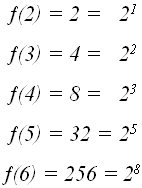
Обозначив через Fn - n-ое число Фибоначчи, имеем: f(n)=
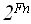.Рекурсивная реализация алгоритмов
Большинство современных языков высокого уровня поддерживают механизм рекурсивного вызова, когда функция, как элемент структуры языка программирования, возвращающая вычисленное значение по своему имени, может вызывать сама себя с другим аргументом. Эта возможность позволяет напрямую реализовывать вычисление рекурсивно определенных функций. Отметим, что в силу тезиса Черча–Тьюринга аппарат рекурсивных функций Черча равномощен машине Тьюринга, и, следовательно, любой рекурсивный алгоритм может быть реализован итерационно.
F(n);
If n=0 or n=1 (проверка возможности прямого вычисления)
Then
F <-- 1
Else
F <-- n*F(n-1); ( рекурсивный вызов функции)
Return (F);
End;Анализ трудоемкости рекурсивных реализаций алгоритмов, очевидно, связан как с количеством операций, выполняемых при одном вызове функции, так и с количеством таких вызовов. Графическое представление порождаемой данным алгоритмом цепочки рекурсивных вызовов называется деревом рекурсивных вызовов. Более детальное рассмотрение приводит к необходимости учета затрат как на организацию вызова функции и передачи параметров, так и на возврат вычисленных значений и передачу управления в точку вызова.
Можно заметить, что некоторая ветвь дерева рекурсивных вызовов обрывается при достижении такого значения передаваемого параметра, при котором функция может быть вычислена непосредственно. Таким образом, рекурсия эквивалентна конструкции цикла, в котором каждый проход есть выполнение рекурсивной функции с заданным параметром.
Рассмотрим пример для функции вычисления факториала (рис 8.1):
Цепочка рекурсивных возвратов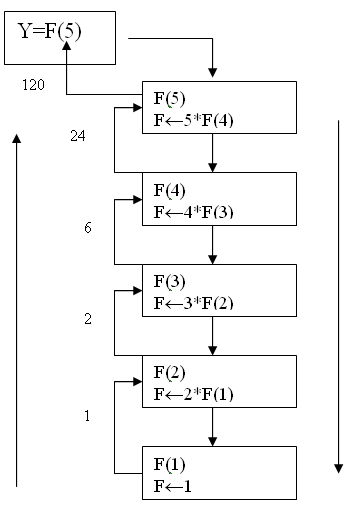 
Цепочка рекурсивных вызовов Рис 8.1 Дерево рекурсии при вычислении факториала – F(5)
Дерево рекурсивных вызовов может иметь и более сложную структуру, если на каждом вызове порождается несколько обращений – фрагмент дерева рекурсий для чисел Фибоначчи представлен на рис 8.2:
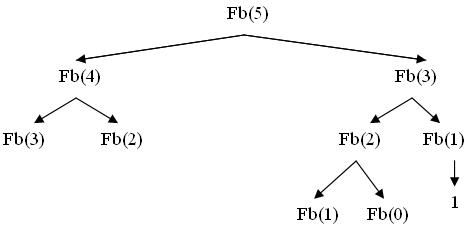
Рис 8.2 Фрагмент дерева рекурсии при вычислении чисел Фибоначчи – F(5)
Анализ трудоемкости механизма вызова процедуры
Механизм вызова функции или процедуры в языке высокого уровня существенно зависит от архитектуры компьютера и операционной системы. В рамках IBM PC совместимых компьютеров этот механизм реализован через программный стек. Как передаваемые в процедуру или функцию фактические параметры, так и возвращаемые из них значения помещаются в программный стек специальными командами процессора. Дополнительно сохраняются зна-чения необходимых регистров и адрес возврата в вызывающую процедуру. Схематично этот механизм иллюстрирован на рис 8.3:
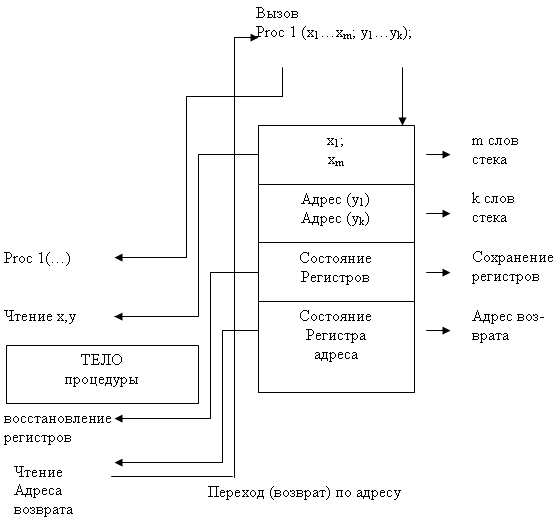
Рис 8.2 Механизм вызова процедуры с использованием программного стека
Для подсчета трудоемкости вызова будем считать операции помещения слова в стек и выталкивания из стека элементарными операциями в формальной системе. Тогда при вызове процедуры или функции в стек помещается адрес возврата, состояние необходимых регистров процессора, адреса возвращаемых значений и передаваемые параметры. После этого выполняется переход по адресу на вызываемую процедуру, которая извлекает переданные фактические параметры, выполняет вычисления, помещает их по указанным в стеке адресам, и при завершении работы восстанавливает регистры, выталкивает из стека адрес возврата и осуществляет переход по этому адресу.
Обозначив через:
m - количество передаваемых фактических параметров,
k - количество возвращаемых процедурой значений,
r - количество сохраняемых в стеке регистров,
имеем:fвызова = m+k+r+1+m+k+r+1 = 2*(m+k+r+1) элементарных операций на один вызов и возврат.
Анализ трудоемкости рекурсивных алгоритмов в части трудоемкости самого рекурсивного вызова можно выполнять разными способами в зависимости от того, как формируется итоговая сумма элементарных операций – рассмотрением в отдельности цепочки рекурсивных вызовов и возвратов, или совокупно по вершинам дерева рекурсивных вызовов.
Анализ трудоемкости алгоритма вычисления факториала
Для рассмотренного выше рекурсивного алгоритма вычисления факториала количество вершин рекурсивного дерева равно, очевидно, n, при этом передается и возвращается по одному значению (m=1, k=1), в предположении о сохранении четырех регистров – r=4, а на последнем рекурсивном вызове значение функции вычисляется непосредственно – в итоге:
fa(n)=n*2*(1+1+4+1)+(n-1)*(1+3)+1*2=18*n - 2
Отметим, что n – параметр алгоритма, а не количество слов на входе.
