Теория алгоритмов
Рекурсивные алгоритмы и методы их анализа
Логарифмические тождества
При анализе рекурсивных алгоритмов достаточно часто используются логарифмические тождества, далее предполагается, что, a > 0, b > 0, c > 0, основание логарифма не равно единице:
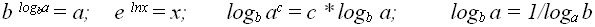
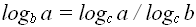
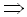
в записи Q(ln(x)) основание логарифма не существенно, если он больше единицы, т.к. константа скрывается обозначением Q.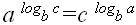
Можно показать, что для любого
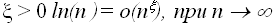
Методы решения рекурсивных соотношений
В математике разработан ряд методов, с помощью которых можно получить явный вид рекурсивно заданной функции – метод индукции, формальные степенные ряды, метод итераций и т.д. Рассмотрим некоторые из них:
а) Метод индукцииМетод состоит в том, что бы сначала угадать решение, а затем доказать его правильность по индукции. Пример:
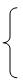
f(0)=1
f(n+1)=2*f(n)Предположение: f(n)=
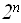
Базис: если f(n)=
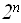 , то f(0)=1, что выполнено по определению.
, то f(0)=1, что выполнено по определению.Индукция: Пусть f(n)=
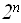 , тогда для n+1
, тогда для n+1 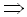 f(n+1)= 2 *
f(n+1)= 2 * 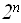 =
=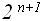
Заметим, что базис существенно влияет на решение, так, например:
Если f(0)=0, то f(n)=0;
если f(0)=1/7, то f(n)=(1/7)*
б) Метод итерации (подстановки)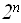 ; если f(0)=1/64, то f(n)=(2)
; если f(0)=1/64, то f(n)=(2)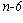
Суть метода состоит в последовательной подстановке – итерации рекурсивного определения, с последующим выявлением общих закономерностей:
Пусть f(n)=3*f(n/4)+n, тогда:
f(n)=n+3*f(n/4)=n+3*[n/4+3*f(n/16)]=n+3*[n/4+3{n/16+3*f(n/64) }],
и раскрывая скобки, получаем:
f(n)=n+3*n/4+9*n/16+27*n/64+…+
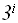 *n/
*n/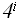
Остановка рекурсии произойдет при
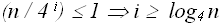 , в этом случае последнее слагаемое не больше, чем
, в этом случае последнее слагаемое не больше, чем 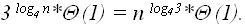
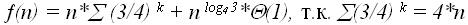 , то окончательно:
, то окончательно: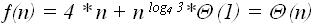
Рекурсивные алгоритмы.
Основной метод построения рекурсивных алгоритмов – это метод декомпозиции. Идея метода состоит в разделении задачи на части меньшей размерности, получение решение для полученных частей и объединение решений.
общем виде, если происходит разделение задачи на b подзадач, которое приводит к необходимости решения a подзадач размерностью n/b, то общий вид функции трудоемкости имеет вид:
fA(n )= a * fA( n/b )+d(n)+U(n) (9.1), где:
d(n) – трудоемкость алгоритма деления задачи на подзадачи,
U(n) – трудоемкость алгоритма объединения полученных решений.Рассмотрим, например, известный алгоритм сортировки слиянием, принадлежащий Дж. Фон Нейману:
На каждом рекурсивном вызове переданный массив делится пополам, что дает оценку для d(n) =Q (1), далее рекурсивно вызываем сортировку полученных массивов половинной длины (до тех пор, пока длина массива не станет равной единице), и сливаем возвращенные отсортированные массивы за Q (n).
Тогда ожидаемая трудоемкость на сортировку составит:
fA(n )= 2 * fA( n/2 )+ Q (1)+ Q (n)Тем самым возникает задача о получении оценки сложности функции трудоемкости, заданной в виде (9.1), для произвольных значений a и b.
Основная теорема о рекуррентных соотношениях
Следующая теорема принадлежит Дж. Бентли, Д. Хакен и Дж. Саксу (1980 г.).
Теорема.Пусть a >= 1, b > 1 - константы, g(n) - функция, пусть далее:
f(n)=a*f(n/b)+g(n)
Тогда:Если g(n)=O(
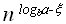 ),
),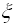 >0, то f(n)=Q(
>0, то f(n)=Q(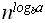 )
)
Пример:f(n) = 8f(n/2)+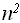 , тогда f(n) = Q(
, тогда f(n) = Q(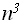 )
)) Если g(n)=Q(
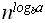 ), то f(n)=Q(
), то f(n)=Q(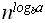 *log n)
*log n)
Пример: fA(n)= 2 * fA( n/2 )+ Q (n), тогда f(n) = Q(n*log n)Если g(n) =
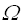 (
(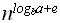 ), e > 0, то f(n)=Q(g(n))
), e > 0, то f(n)=Q(g(n))
Пример: f(n)=2*f(n/2)+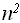 , имеем:
, имеем:
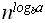 =
= 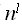 , и следовательно: f(n) = Q(
, и следовательно: f(n) = Q(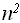 )
)Данная теорема является мощным средством анализа асимптотической сложности рекурсивных алгоритмов, к сожалению, она не дает возможности получить полный вид функции трудоемкости.

