Теория алгоритмов
Трудоемкость алгоритмов и временные оценки
Элементарные операции в языке записи алгоритмов
Для получения функции трудоемкости алгоритма, представленного в формальной системе введенной абстрактной машины необходимо уточнить понятия «элементарных» операций, соотнесенных с языком высокого уровня.
-
В качестве таких «элементарных» операций предлагается использовать следующие:
Простое присваивание: а <-- b;
Одномерная индексация a[i] : (адрес (a)+i*длинна элемента);
Арифметические операции: (*, /, -, +);
Операции сравнения: a < b;
Логические операции (l1) {or, and, not} (l2);
Опираясь на идеи структурного программирования, исключим команду перехода по адресу, считая ее связанной с операцией сравнения в конструкции ветвления.
-
После введения элементарных операций анализ трудоемкости основных алгоритмических конструкций в общем виде сводится к следующим положениям:
Конструкция «Следование»
Трудоемкость конструкции есть сумма трудоемкостей блоков, следующих друг за другом. 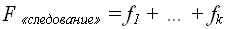 , где k – количество блоков.
, где k – количество блоков.Конструкция «Ветвление»
if( l ) then 
else 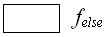
Общая трудоемкость конструкции «Ветвление» требует анализа вероятности выполнения переходов на блоки «Then» и «Else» и определяется как:
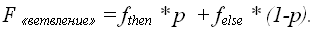
Конструкция «Цикл»
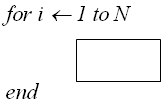
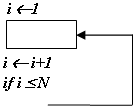
После сведения конструкции к элементарным операциям ее трудоемкость определяется как:
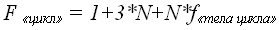
Примеры анализа простых алгоритмов
Пример 1 Задача суммирования элементов квадратной матрицы
SumM (A, n; Sum)
Sum <-- 0
For i <-- 1 to n
For j <-- 1 to n
Sum <-- Sum + A[i,j]
end for
Return (Sum)
EndАлгоритм выполняет одинаковое количество операций при фиксированном значении n, и следовательно является количественно-зависимым. Применение методики анализа конструкции «Цикл » дает:
 (n)=1+1+ n *(3+1+ n *(3+4))=7
(n)=1+1+ n *(3+1+ n *(3+4))=7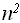 +4* n +2 =
+4* n +2 = 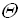 (
(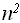 ) заметим, что под n понимается линейная размерность матрицы, в то время как на вход алгоритма подается
) заметим, что под n понимается линейная размерность матрицы, в то время как на вход алгоритма подается 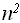 значений.
значений.Пример 2 Задача поиска максимума в массиве
MaxS (S,n; Max)
Max <-- S[1]
For i <-- 2 to n
if Max < S[i]
then Max <-- S[i]
end for
return Max
EndДанный алгоритм является количественно-параметрическим, поэтому для фиксированной размерности исходных данных необходимо проводить анализ для худшего, лучшего и среднего случая.
А). Худший случай
Максимальное количество переприсваиваний максимума (на каждом проходе цикла) будет в том случае, если элементы массива отсортированы по возрастанию. Трудоемкость алгоритма в этом случае равна:
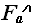 (n)=1+1+1+ (n-1) (3+2+2)=7 n - 4 =
(n)=1+1+1+ (n-1) (3+2+2)=7 n - 4 = 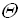 (n).
(n).Б) Лучший случай
Минимальное количество переприсваивания максимума (ни одного на каждом проходе цикла) будет в том случае, если максимальный элемент расположен на первом месте в массиве. Трудоемкость алгоритма в этом случае равна:
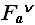 (n)=1+1+1+ (n-1) (3+2)=5 n - 2 =
(n)=1+1+1+ (n-1) (3+2)=5 n - 2 = 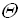 (n).
(n).В) Средний случай
Алгоритм поиска максимума последовательно перебирает элементы массива, сравнивая текущий элемент массива с текущим значением максимума. На очередном шаге, когда просматривается к-ый элемент массива, переприсваивание максимума произойдет, если в подмассиве из первых к элементов максимальным элементом является последний. Очевидно, что в случае равномерного распределения исходных данных, вероятность того, что максимальный из к элементов расположен в определенной (последней) позиции равна 1/к. Тогда в массиве из n элементов общее количество операций переприсваивания максимума определяется как:
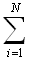
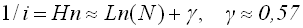
Величина Hn называется n-ым гармоническим числом. Таким образом, точное значение (математическое ожидание) среднего количества операций присваивания в алгоритме поиска максимума в массиве из n элементов определяется величиной Hn (на бесконечности количества испытаний), тогда:
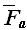 (n)=1 + (n-1) (3+2) + 2 (Ln(n) +
(n)=1 + (n-1) (3+2) + 2 (Ln(n) + 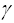 )=5 n +2 Ln(n) - 4 +2
)=5 n +2 Ln(n) - 4 +2 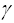 =
= 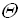 (n).
(n).Переход к временным оценкам
Сравнение двух алгоритмов по их функции трудоемкости вносит некоторую ошибку в получаемые результаты. Основной причиной этой ошибки является различная частотная встречаемость элементарных операций, порождаемая разными алгоритмами и различие во временах выполнения элементарных операций на реальном процессоре. Таким образом, возникает задача перехода от функции трудоемкости к оценке времени работы алгоритма на конкретном процессоре:
Дано:
 (
(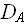 ) - трудоёмкость алгоритма требуется определить время работы программной реализации алгоритма –
) - трудоёмкость алгоритма требуется определить время работы программной реализации алгоритма – 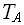 (
(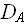 ).
).-
На пути построения временных оценок мы сталкиваемся с целым набором различных проблем, пофакторный учет которых вызывает существенные трудности. Укажем основные из этих проблем:
неадекватность формальной системы записи алгоритма и реальной системы команд процессора;
наличие архитектурных особенностей существенно влияющих на наблюдаемое время выполнения программы, таких как конвейер, кеширование памяти, предвыборка команд и данных, и т.д.;
различные времена выполнения реальных машинных команд;
различие во времени выполнения одной команды, в зависимости от значений операндов
различные времена реального выполнения однородных команд в зависимости от типов данных;
неоднозначности компиляции исходного текста, обусловленные как самим компилятором, так и его настройками.
Попытки различного подхода к учету этих факторов привели к появлению разнообразных методик перехода к временным оценкам.
1) Пооперационный анализ
Идея пооперационного анализа состоит в получении пооперационной функции трудоемкости для каждой из используемых алгоритмом элементарных операций с учетом типов данных. Следующим шагом является экспериментальное определение среднего времени выполнения данной элементарной операции на конкретной вычислительной машине. Ожидаемое время выполнения рассчитывается как сумма произведений пооперационной трудоемкости на средние времена операций:
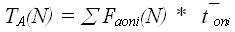
2) Метод Гиббсона
-
Метод предполагает проведение совокупного анализа по трудоемкости и переход к временным оценкам на основе принадлежности решаемой задачи к одному из следующих типов:
задачи научно-технического характера с преобладанием операций с операндами действительного типа;
задачи дискретной математики с преобладанием операций с операндами целого типа
задачи баз данных с преобладанием операций с операндами строкового типа
Далее на основе анализа множества реальных программ для решения соответствующих типов задач определяется частотная встречаемость операций (рис 5.1), создаются соответствующие тестовые программы, и определяется среднее время на операцию в данном типе задач –
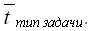
Рис 5.1 Возможный вид частотной встречаемости операцийНа основе полученной информации оценивается общее время работы алгоритма в виде:
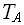 (N) =
(N) =  (N) *
(N) *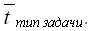
3) Метод прямого определения среднего времени
В этом методе так же проводится совокупный анализ по трудоемкости – определяется
 (N), после чего на основе прямого эксперимента для различных значений
(N), после чего на основе прямого эксперимента для различных значений 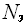 определяется среднее время работы данной программы
определяется среднее время работы данной программы 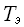 и на основе известной функции трудоемкости рассчитывается среднее время на обобщенную элементарную операцию, порождаемое данным алгоритмом, компилятором и компьютером –
и на основе известной функции трудоемкости рассчитывается среднее время на обобщенную элементарную операцию, порождаемое данным алгоритмом, компилятором и компьютером – 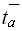 . Эти данные могут быть (в предположении об устойчивости среднего времени по N) интерполированы или экстраполированы на другие значения размерности задачи следующим образом:
. Эти данные могут быть (в предположении об устойчивости среднего времени по N) интерполированы или экстраполированы на другие значения размерности задачи следующим образом: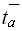 =
= 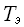 (
(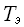 ) /
) /  (
(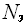 ), T(N) =
), T(N) = 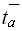 *
*  (N).
(N).Пример пооперационного временного анализа
В ряде случаев именно пооперационный анализ позволяет выявить тонкие аспекты рационального применения того или иного алгоритма решения задачи. В качестве примера рассмотрим задачу умножения двух комплексных чисел:
(a+bi)*(c+di)=(ac - bd) + i(ad + bc)=e + if
- Алгоритм А1 (прямое вычисление e, f – четыре умножения)
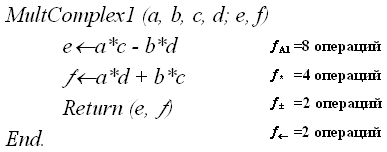
- Алгоритм А2 (вычисление e, f за три умножения)
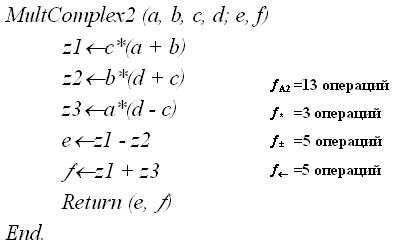
Пооперационный анализ этих двух алгоритмов не представляет труда, и его результаты приведены справа от записи соответствующих алгоритмов.
По совокупному количеству элементарных операций алгоритм А2 уступает алгоритму А1, однако в реальных компьютерах операция умножения требует большего времени, чем операция сложения, и можно путем пооперацион-ного анализа ответить на вопрос: при каких условиях алгоритм А2 предпочтительнее алгоритма А1?
Введем параметры q и r, устанавливающие соотношения между временами выполнения операции умножения, сложения и присваивания для операндов действительного типа.
Тогда мы можем привести временные оценки двух алгоритмов к времени выполнения операции сложения/вычитания –
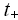 :
: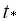 = q*
= q*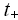 , q>1;
, q>1;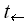 =r*
=r*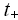 , r<1, тогда приведенные к
, r<1, тогда приведенные к 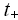 временные оценки имеют вид:
временные оценки имеют вид: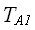 = 4*q*
= 4*q*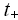 +2*
+2*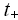 +2*r*
+2*r*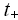 =
=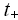 *(4*q+2+2*r);
*(4*q+2+2*r);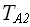 = 3*q*
= 3*q*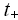 +5*
+5*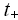 +5*r*
+5*r*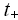 =
=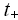 *(3*q+5+5*r).
*(3*q+5+5*r).Равенство времен будет достигнуто при условии:
4*q+2+2*r = 3*q+5+5*r, откуда:
q = 3 + 3r и следовательно при q > 3 + 3r алгоритм А2 будет работать более эффективно.Таким образом, если среда реализации алгоритмов А1 и А2 – язык программирования, обслуживающий его компилятор и компьютер на котором реализуется задача – такова, что время выполнения операции умножения двух действительных чисел более чем втрое превышает время сложения двух действительных чисел, в предположении, что r << 1, а это реальное соотношение, то для реализации более предпочтителен алгоритм А2.
Конечно, выигрыш во времени пренебрежимо мал, если мы перемножаем только два комплексных числа, однако, если этот алгоритм является частью сложной вычислительной задачи с комплексными числами, требующей существенно значимого по времени количества умножений, то выигрыш во времени может быть ощутим. Оценка такого выигрыша на одно умножение комплексных чисел следует из только что проведенного анализа:
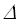 T = (q – 3 – 3*r)*
T = (q – 3 – 3*r)* 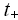
- Алгоритм А1 (прямое вычисление e, f – четыре умножения)

